-
Sándorné Szatmári: @mederi: 11 Kiegészítem a korábbi, mederi néven írt megjegyzésemet.. Ami a cikkben is kife...2025. 06. 05, 13:16 Falánk igék
-
nasspolya: @ganajtúrós bukta: www.reddit.com/r/linguisticshumor/s/BuJhBlK4t82025. 06. 01, 01:06 „Mert nincs rá szó, nincsen rá...
-
Sándorné Szatmári: @szigetva: Korábban számos valóban értelmetlen bejegyzések és viták fóruma is volt helyenk...2025. 05. 18, 16:36 „Mert nincs rá szó, nincsen rá...
-
szigetva: @Sándorné Szatmári: A viták az új cikkek hiánya és a vitaképes kommentelők elmaradása miat...2025. 05. 14, 10:56 „Mert nincs rá szó, nincsen rá...
-
Sándorné Szatmári: @Sándorné Szatmári: 43 Remélem, hogy a 43. hozzászólást már nem törlitek (.. ezt is mentet...2025. 05. 14, 08:39 „Mert nincs rá szó, nincsen rá...
Kálmán László nyelvész, a nyest szerkesztőségének alapembere, a hazai nyelvtudomány és nyelvi ismeretterjesztés legendás alakjának rovata volt ez.
- Elhunyt Kálmán László, a Nyelvész, aki megmondja
- Így műveld a nyelvedet
- Utoljára a bicigliről
- Start nyelvstratégia!
- Változás és „igénytelenség”
Kálmán László korábbi cikkeit itt találja.

Ha legutóbb kimaradt, most itt az új lehetőség!
Ha ma csak egyetlen nyelvészeti kísérletben vesz részt, mindenképp ez legyen az!
Finnugor nyelvrokonság: hazugság
A határozott névelő, ami azt jelenti, hogy ‘te’
Az oroszok már a fejünkön vannak!
A napisajtóban gyakran emlegetik a mérés hibahatárát, ha közvélemény-kutatásokról van szó, de néha mégis félreértik ezt a fogalmat. Lehet, hogy szándékosan magyarázzák félre, hogy így csalhassanak a statisztikával? Hogyan értelmezzük mi magunk a közvélemény-kutatásokat?
Korábban már többször írtunk arról, hogyan lehet trükközni a grafikonokkal, számokkal, és milyen módokon lehet még félrevezetni az embereket a statisztika rafinált felhasználásával. Most egy olyan témáról lesz szó, ami első pillantásra kicsit technikaibbnak tűnhet, de valójában az újsághírekben is gyakran előkerül...

(Forrás: Wikimedia Commons / Czank Máté)
Beismeri a hibáját?
Mindenféle mérésnek van hibája is. Ez természetes, nem kell tőle megijedni! Nem arról van szó, mint amit a hétköznapi életben értünk hiba alatt, tehát hogy valamit elrontottunk. Ha egy tudós mérési hibáról beszél, az nem feltétlenül azt jelenti, hogy a mérés úgy rossz, ahogy van, és lehet az elejéről kezdeni az egészet. De akkor mit jelent?
A kutatók többféle hibát különböztetnek meg. A két legnagyobb csoport a rendszeres és a véletlen hibák csoportja. Ha fogunk egy szobamérleget és ráteszünk egy ötkilós követ, akkor bárki áll rá, a mérleg következetesen öt kilóval nagyobbnak fogja mutatni a testtömegét – az ilyen és hasonló, minden mérést egy irányba torzító tényezők okozta hibákat hívják rendszeres hibának. (A hétköznapi nyelvben valami ilyesmit szokás a 'mérési hiba' megfogalmazás mögé odaképzelni.) De ha a rendszeres hibáktól többé-kevésbé megszabadultunk, még mindig ott a véletlen hiba: ez sok kis különböző, összevissza ható tényező eredménye, és nem lehet teljesen kiküszöbölni.
Az oldal az ajánló után folytatódik...
Ha valamit többször egymás után lemérünk, nem pontosan ugyanazt az eredményt kapjuk – ha nem hisszük, próbáljunk meg ötször egymás után ráállni a szobamérlegre! Lehet, hogy egyszer hatvan kilót mutat, majd ötvenkilencet, majd megint hatvanat, és így tovább. Ez az ingadozás, a véletlen hiba független attól, hogy észrevettük-e és levettük-e a mérlegről az előző használó által gondosan odakészített ötkilós követ... A véletlen hiba teljesen természetes dolog, és a statisztikusok tudnak vele bánni. Lássuk, hogyan! (A következőkben, ha csak külön nem említjük, mindig a véletlen hibáról lesz szó.)
Illeg-billeg
A hiba azt mutatja, mekkora a bizonytalanság a kapott eredményekben. Ha például rendre 60; 64; 56; 60; 61 kilóra adódott a testtömegünk, akkor a hiba nagyobb, mint ha mondjuk a 60; 61; 60; 59; 61 kilókat kapnánk: az értékek jobban eltérnek egymástól. (A két sorozat átlaga megegyezik.)
A gyakorlatban a közvéleménykutatások néhány százas vagy ezres mintával dolgoznak. Néhány újabb példa különböző sajtótermékekből: 500 osztrákot kérdeztek meg arról, hogyan viszonyulnak az EU-integrációhoz; 1581 republikánust kérdeztek arról, támogatnák-e Herman Cain elnökjelöltségét (ez még azelőtt volt, hogy visszalépett volna); 1000 magyart pedig arról faggattak, együttműködik-e az MSZP és a Demokratikus Koalíció.
Minél többet mérünk, annál kisebb a véletlen hiba – a számos apró, más-más irányba mutató különbség kiegyenlíti egymást. Arról már korábban írtunk, hogy a nagy mintaelemszám önmagában nem jelent semmit, és sokkal fontosabb a reprezentativitás. Emlékeztetőül: hiába töltetünk ki egy szekérderéknyi kérdőívet a barátainkkal, az nem biztos, hogy bármit is mond a magyar lakosságról. De ha a mintánk a lehetőségekhez képest reprezentatív, akkor igenis számít az elemszám. Lehet egy tíz fős minta is reprezentatív, meg egy tízezres is, de az utóbbinak kisebb lesz a hibája.
Sávom, sávom, mondd meg nékem
A hibahatár mutatja meg, mekkora eltérés lehet a valódi és a mért érték között. A mindennapokban ez az, ami igazán fontos, hiszen az, hogy „az átlag standard hibája 3,562”, legfeljebb egy szakmabelinek mond valamit. A hibahatár viszont előtanulmányok nélkül értelmezhető: azt mondja ki, hogy a legvalószínűbben milyen sávon belül esnek az eredmények (ez a hibasáv). Hogy megfoghatóbb legyen ez az absztrakt fogalom, lássunk egy szemléletes kitalált példát!
A Bergengóc Népi-Nemzeti Közvéleménykutató Intézet mérése azt mutatja, hogy a bergengócnyelv-tanárok 48%-a szerint igen elavult a bergengóc nyelv helyesírási szabályzata. (Nincsenek vele egyedül.) A hibahatár plusz-mínusz 4%, tehát ez azt jelenti, hogy a valóságban a tanárok 44-52%-a vélekedik így. Lehet, hogy csak 45%-uk, de az is lehet, hogy 52%-uk. Az viszont a mérés fényében nagyon valószínűtlen és nyugodtan elvethető, hogy a tanárok 20%-a vagy 75%-a képviseli ezt az álláspontot.
Mindig fennáll annak az esélye, hogy a hibahatáron kívül esik a valódi érték. Például ha Magyarországon tíz olyan ember van, aki harminc nyelvet beszél, és tíz fős reprezentatív mintával vizsgáljuk a magyarok nyelvtudását, akkor nagyon pici eséllyel ugyan, de lehet, hogy pont ezt a tíz embert választjuk ki véletlenszerűen... és aztán megállapítjuk, hogy az átlag magyar harminc nyelven beszél. A hibasáv lényege épp az, hogy nagy valószínűséggel belekerül a valódi érték, de a nagy valószínűség nem jelent teljes bizonyosságot.
Pirx pilóta kalandjai
Sok újság megírja a közvéleménykutatások hibahatárát – a fenti oldaldoboz osztrák, amerikai és magyar példái mind tartalmazzák ezt az adatot is. De milyen hibahatár számít jónak? A bevett módszerekkel végzett közvéleménykutatások hibahatára plusz-mínusz 3-5% körüli szokott lenni. Ha nagyon titkolják a hibahatárt, az valószínűleg azért van, mert túl magas! A plusz-mínusz (±) jelet pedig olykor bevallottan elfelejtik kitenni...
Ha nem közvéleménykutatásról van szó, arra érdemes gondolni, mekkora bizonyosságra van szükség a konkrét esetben. Stanisław Lem klasszikus sci-fi elbeszélése, A teszt épp erre mutat rá:
De a pálya kis híján érinti a Holdat. Nem tudni, hogy átsiklik-e az űrhajó a Hold fölött, vagy belefúródik. A trajektométer hibahatára hét-nyolc kilométer – lehet a görbe alsó pontja három kilométerrel a sziklák fölött, vagy ugyanannyival alattuk.
Ha Pirx pilóta jó ezer kilométer távolságban repül a Holdtól, nem nagyon számít neki, hogy 1003 vagy 1004 kilométer messze van az űrhajója az égitesttől, tehát ez a hibahatár teljesen megfelelő számára. De ha épp a Hold közvetlen közelében jár az űrhajójával, mindjárt élet-halál kérdése a három és négy kilométer közötti különbség! (Ha valakit érdekel, mi történik ezután a kétségbeejtő helyzetbe került Pirx pilótával, az interneten fenn van a novella teljes szövege, a Beleolvasok gombra kell kattintani.)
Csalás és ámítás
A tudományos közleményekben sokféle grafikonra szokás hibasávot rakni. A hibasáv terjedelmét többféle módszerrel is ki lehet számolni, ilyenkor – jobb esetben – a cikk szövegéből kiderül, milyen módszert használtak a kutatók. A napisajtóban ellenben hibasávot szinte sosem látni, még akkor sem, amikor a cikk szövege említi a hibahatárt. Ha olvasóink találkoznak vadon élő hibasávval, küldjék be a képet, hadd örüljünk neki együtt!
Mutatunk egy valódi vizsgálatból származó példát. Ez az ábra egy olyan vizsgálatból származik, amelyben azt hasonlították össze, mennyire jól tudnak tájékozódni különböző szerkezetű weblapokon a fiatalok és az idősek. Egy hierarchikus szerkezetű és egy címkéket használó weblapon kellett előre megadott kérdésekre választ keresni. Az ábrán bal oldalt a hierarchikus, jobb oldalt a címkéket használó weblapon elért eredmények láthatóak. A piros színű oszlopok az idősek, a kékek a fiatalok teljesítményét mutatják. A függőleges pöckök jelölik a hibasávokat – a szakasz két végpontja (a pöckök feje) mutatja a sáv egyik és másik végét a függőleges tengelyen.
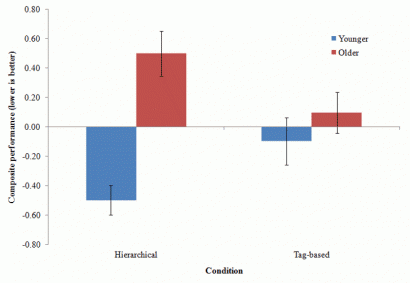
(Forrás: Pak R, Price MM, Thatcher J / CC BY 2.0)
A bal oldalon, azaz a hierarchikus weblap esetében nagy különbség van a fiatalok és az idősek között. (Kicsit szokatlan módon az Y tengelyen a nagyobb értékek rosszabb teljesítményt jelölnek, de erre az Y tengely
angol nyelvű felirata felhívja a figyelmet. Tehát a fiatalok teljesítménye
jobb.) A hibasávok között nincs átfedés, látványosan elkülönülnek
egymástól – a mért különbség valószínűleg valós.
Viszont a címkéket használó weblap esetében a fiatalok és az idősek között ugyan mértek egy kis különbséget, de a hibasávok nagy mértékben átfedik egymást, így lehet, hogy valójában nincs is a két csoport között eltérés. (A cikkben részletesen kifejtett statisztikai számítások tényleg azt mutatták, hogy a címkés weblap használata során a fiatalok és az idősek között nincsen szignifikáns teljesítménykülönbség.) Láthatjuk, hogy még egy egyszerű oszlopdiagramnál is hasznos információt nyújt a hibasávok feltüntetése!
Miért lehet baj, ha nincs a grafikonokon hibasáv? Azért, mert a lelkes olvasó azt gondolhatja, az eredmény jobb, mint valójában. Ha az ábrán nem találunk a grafikonnal való csalásokról szóló cikkünkben bemutatott durva félrevezetéseket, örömmel állapíthatjuk meg, hogy minden szép és jó. De a valóságban lehet, hogy az eredmények körüli bizonytalanság olyan nagy, hogy az ábrából igazából semmilyen következtetést nem lehetne levonni... Ha a hibasávok szerepelnének a képen, akkor ezt rögtön lehetne látni, míg a számadatok fölött reggelizés közben elsiklik az ember szeme.
A leggyakoribb statisztikai csalás, amikor a hibahatáron belüli eltéréseknek jelentést adnak. Ha egy párt támogatottsága 1%-kal nőtt, de a mérés hibahatára 3% (mint egy tipikus közvéleménykutatásnál), akkor az is lehet, hogy a párt támogatottsága egyáltalán nem változott. Mégis láttunk már törtszázalékos növekedést is valós különbségként feltüntetve. Ugyanezen okból nagyon nehéz előre megmondani, kik jutnak be a parlamentbe! Ha a mérés szerint egy pártra 4% szavazna, akkor a közvéleménykutatások megszokott hibahatára mellett lehet, hogy a párt pont az 5%-os parlamenti küszöb alá kerül, de az is, hogy fölé.
További olvasnivalók
Hibasávok típusai, hibasáv felhelyezése táblázatkezelőkkel
Muszáj volt ráraknod a hibasávokat? (karikatúra)
Nézettségmérések és a hibahatár (itt még ritkábban kerül elő, mint a politikai cikkekben...)
Két szakmaibb cikk haladóknak: Error bars in experimental biology / The link between error bars and statistical significance